aptgasil.blogg.se - Arithmetic geometric sequence calculator

Where a1 is the first term of the sequence and n is the position of the term in the sequence. The formula for the nth term of a geometric sequence is: an = a1 * r^(n-1) The ratio of consecutive terms is called the common ratio, denoted by the letter r. Geometric SequencesĪ geometric sequence is a sequence of numbers in which the ratio of any two consecutive terms is always the same.

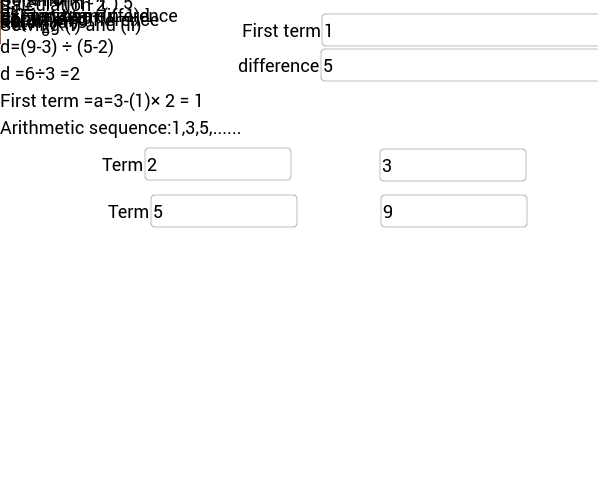
To find the next number in the sequence, we would add 3 to 11, which gives us 14. For example, in sequences 2, 5, 8, and 11, the common difference is 3. We add the common difference to the current term to find the next number in an arithmetic sequence. The formula for the nth term of an arithmetic sequence is: An = a1 + (n - 1)d The difference between consecutive terms is called the common difference, denoted by the letter d. Arithmetic SequencesĪn arithmetic sequence is a sequence of numbers in which the difference between two consecutive terms is always the same. It's also used in many other fields, such as cryptography, genetics, statistics, etc. Economics: modeling macroeconomic and microeconomic systems, financial modeling, finding equilibrium solutions.

Physics and engineering: modeling physical systems, solving differential equations, signal processing.Computer Science: generating unique ids, generating random numbers, generating prime numbers, generating Fibonacci sequence, generating a sequence of binary numbers.

Calculus: finding the limit of a sequence, finding the sum of an infinite series, and solving differential equations.

Algebra: solving recursion and difference equations, finding a closed form of a sequence, finding generating functions, finding the inverse of a sequence.

Number theory: finding the nth term of a sequence, identifying the common difference or ratio of a sequence, determining if a sequence is arithmetic or geometric, summing the terms of a sequence, and analyzing the limit of a sequence.

Sieve of Eratosthenes algorithm: An algorithm efficiently finds all prime numbers up to a given limit.Ī number sequence calculator can be used in various mathematical and scientific fields, such as: Fibonacci sequence: A sequence of numbers where each term is the sum of the two preceding terms, usually starting with 0 and 1.ġ0. Common ratio: The ratio of consecutive terms in a geometric sequence.ĩ.

Geometric sequences: A sequence of numbers in which the ratio of any two consecutive terms is always the same.Ĩ. Common difference: The difference between consecutive terms in an arithmetic sequence.ħ. Arithmetic sequences: A sequence of numbers in which the difference between two consecutive terms is always the same.Ħ. Prime numbers: A natural number greater than one that has no positive divisors other than one and itself.ĥ. Mathematical patterns: Regularities or consistent relationships in mathematical or numerical data.Ĥ. Calculator: A tool used to perform mathematical calculations.ģ. Number sequence: A sequence of numbers that follow a specific pattern or rule.Ģ. In this article, we will explore common types of number sequences and the methods used to calculate the next number in the sequence.ġ. Number sequences can take many forms, such as mathematical patterns, sequences of prime numbers, or sequences of random numbers. A number sequence calculator is a tool used to determine the next number in a sequence of numbers.